Perimeter and Area of Quadrilaterals

Mathematics is known for being a hard and mundane subject. The biggest problem that lead to this reputation is the way it is taught. As a student, you are told to memorize formulas and apply them to homework and tests. Mathematics is much more than that, it is practical life translated into numbers and letters. It is logic. In this article, we’ll guide you to properly explain the Mathematical concepts of perimeter and area of quadrilaterals to your kids, while including fun and practical life learning worksheets from our website.

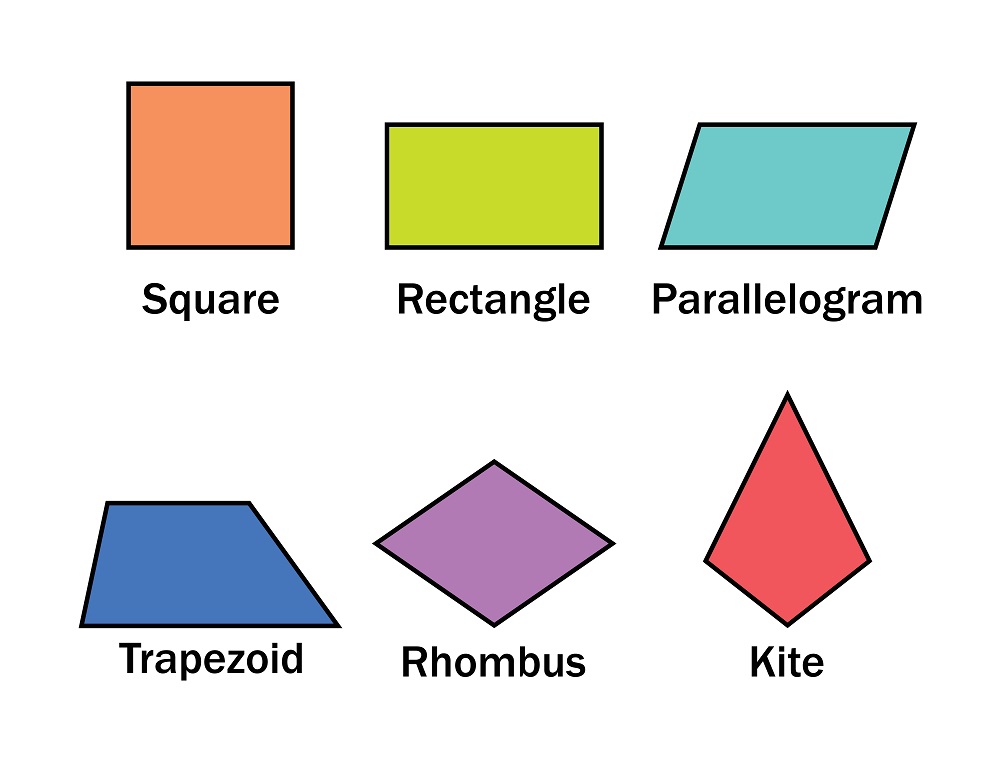
In geometry, there are several shapes to be acquainted with. For this lesson, your kid needs to know the quadrilateral shapes family. The Latin root “Quad” means “four”, so quadrilaterals are the shapes that have four sides. The most common quadrilaterals are:

• Square: A shape with four equal sides and four right angles, with two sets of parallel lines
• Rectangle: The opposite sides of this shape are equal and parallel, with four right angles
• Parallelogram: Like the rectangle, this shape’s opposite sides are equal and parallel, its opposite sides are equal but are not right angles
• Rhombus (diamond): Like the square, this shape has four equal sides and four equal angles but none of them is a right angle

Two concepts that often confuse students are the perimeter and area of a certain shape. For this lesson, we will focus on the perimeter and area of quadrilaterals.

What is Perimeter?

A perimeter is the path that surrounds a certain shape. To calculate the path that surrounds a quadrilateral, we need to get the sum of its four sides, both lengths and widths, lengths being the longest sides and the widths being the shortest. The formula used for calculating perimeter is Perimeter = Length + Length + Width + Width. For instance, to calculate the perimeter of a parallelogram with a side of 5 cm and one of 3 cm, we insert the numbers in their corresponding spot in the formula as such: Perimeter=5+5+3+3=16 cm or since parallelograms have 2 sets of 2 equal sides, we can use this formula Perimeter=(5×2)+(3×2)=10+6=16 cm. For a square on the other hand, we only need to know the length of one side because it has 4 equal sides. Another way to aid the visual learner to understand perimeter is to make use of the Calculating Perimeter Kids Academy video that covers what your child needs to know about the concept.

What is Area?

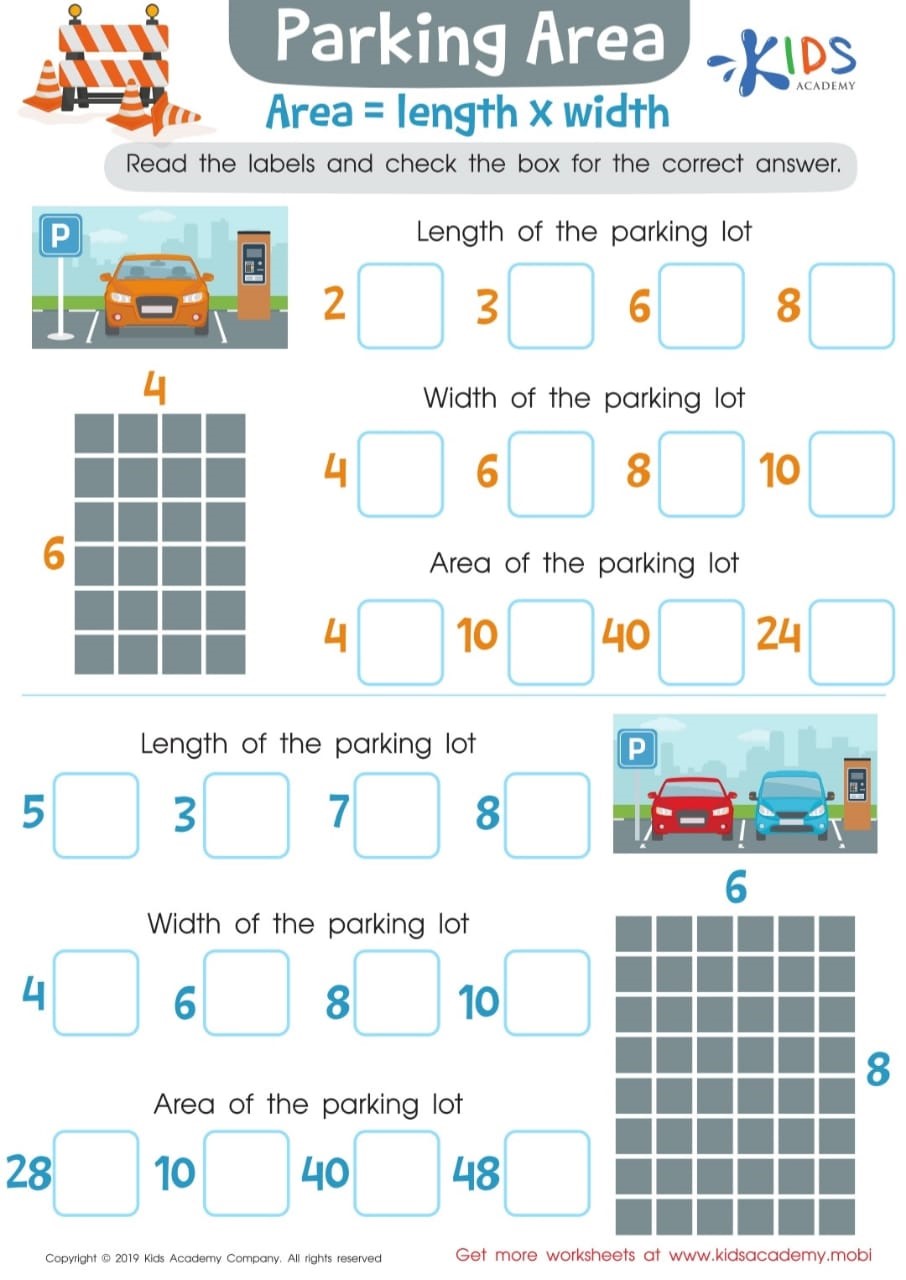
In geometry, area refers to the space occupied by a certain shape, like that of a room’s floor or a door. To determine the area of a quadrilateral, we usually follow the formula of Area = Length × Width. The unit of the area for any two-dimensional shape is always squared. For example, to obtain the area of a rectangle with one side 3cm and one 7cm, we apply the formula 7×3=21cm2. Like in the case of perimeter, we need to know only the length of one side of a square in order to calculate its area.  To simplify this whole process for your third grader, another method can be applied. This method requires us to see how many squares can fit inside the shape. The easiest way to do that is by using a grid. Our worksheet “Parking Area” provides the perfect activity for your kid to apply this method while using a fun example from our daily life, making mathematics seem more approachable and concrete.

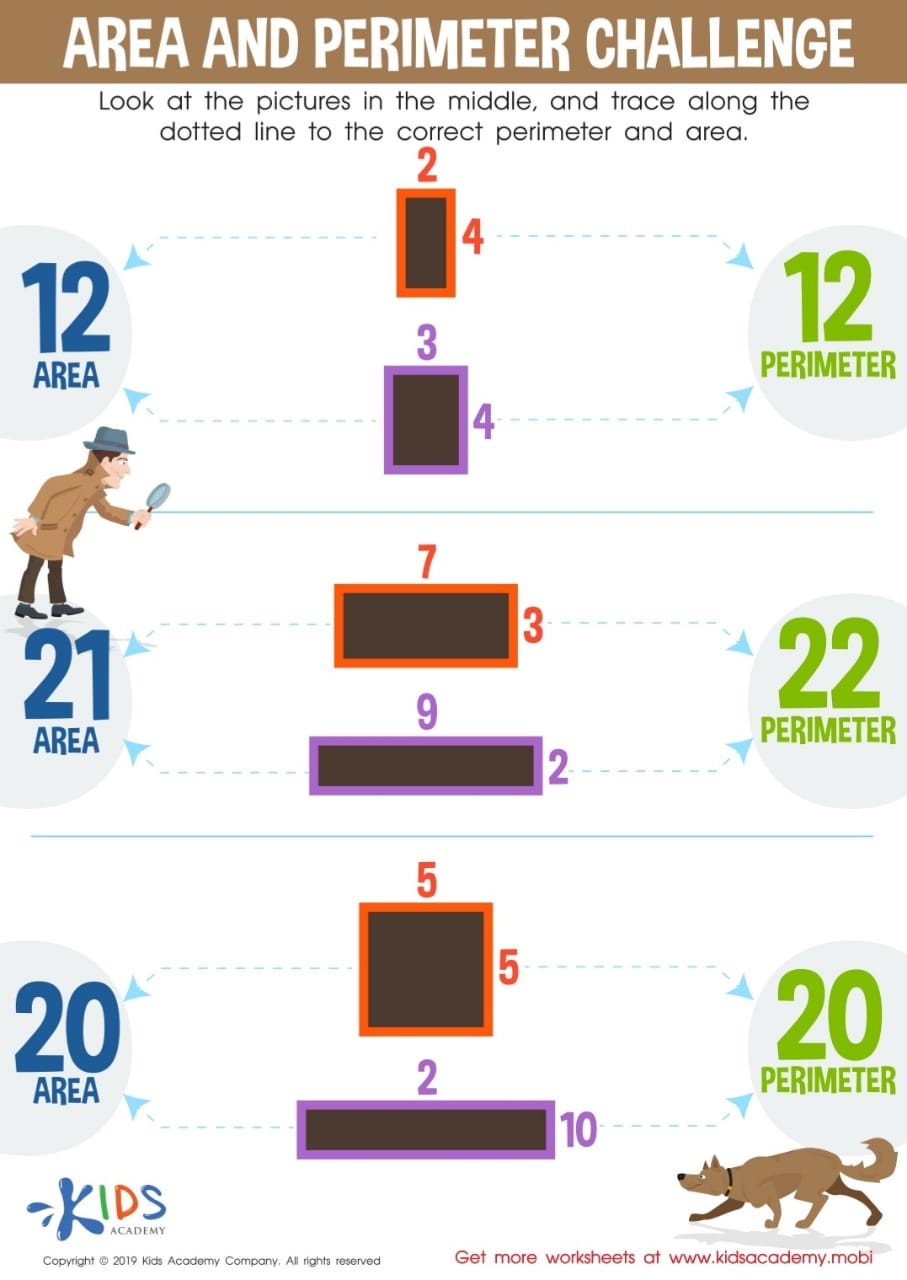
Area or Perimeter?

As has been stated, Math is not an abstract concept, and area and perimeter are not just formulas in the clouds, but can be translated into real life scenarios. But how to know when to use one or the other? As we have established, area is usually used to calculate the space occupied by a shape. For example, in order to cover a room’s floor with a carpet, the area of the floor needs to be calculated. On the other hand, the perimeter measures the boundary of a shape. Thus, if for instance someone needs to decorate their house with Christmas lights, they need to figure out the perimeter of the house in order to get a long enough light. In this worksheet titled “Area and Perimeter Challenge”, your child is presented with a perimeter equal to an area but each corresponding to a different shape.

For example, the first challenge presents them with a 12 perimeter and 12 area, and they should identify which of the two corresponds to which of the given shapes. This exercise will help them further establish both concepts and observe how the same answer can correspond to different shapes. In addition, it helps them practice applying the methods provided in this article.