Understanding fractions Comparing Numbers Worksheets for Ages 5-8
3 filtered results
-
From - To
Discover a fun and engaging way to teach your child about fractions with our "Understanding Fractions Comparing Numbers" worksheets, designed for ages 5-8! These interactive resources help young learners grasp the concept of fractions through colorful illustrations and easy-to-follow activities. Your child will enhance their math skills by comparing different fractions, developing critical thinking, and building a solid foundation for future lessons. Our worksheets cater to various learning styles, ensuring that every child can participate and enjoy the learning process. Start exploring the world of fractions and boost your child's confidence in math today! Perfect for home or classroom use.
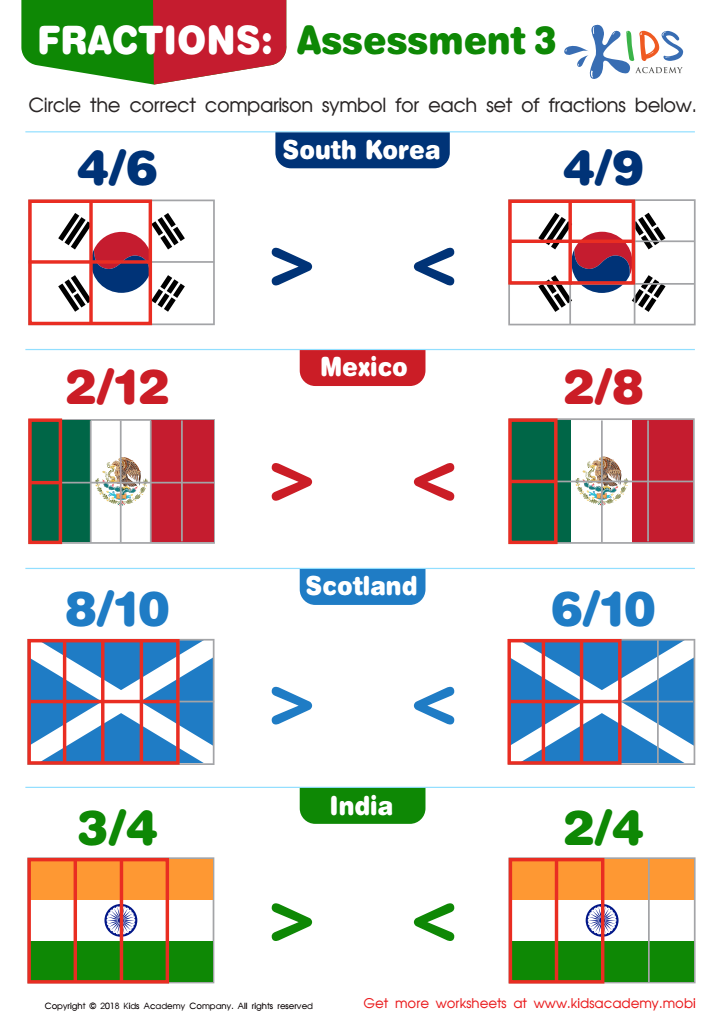

Fractions: Assessment 3 Worksheet
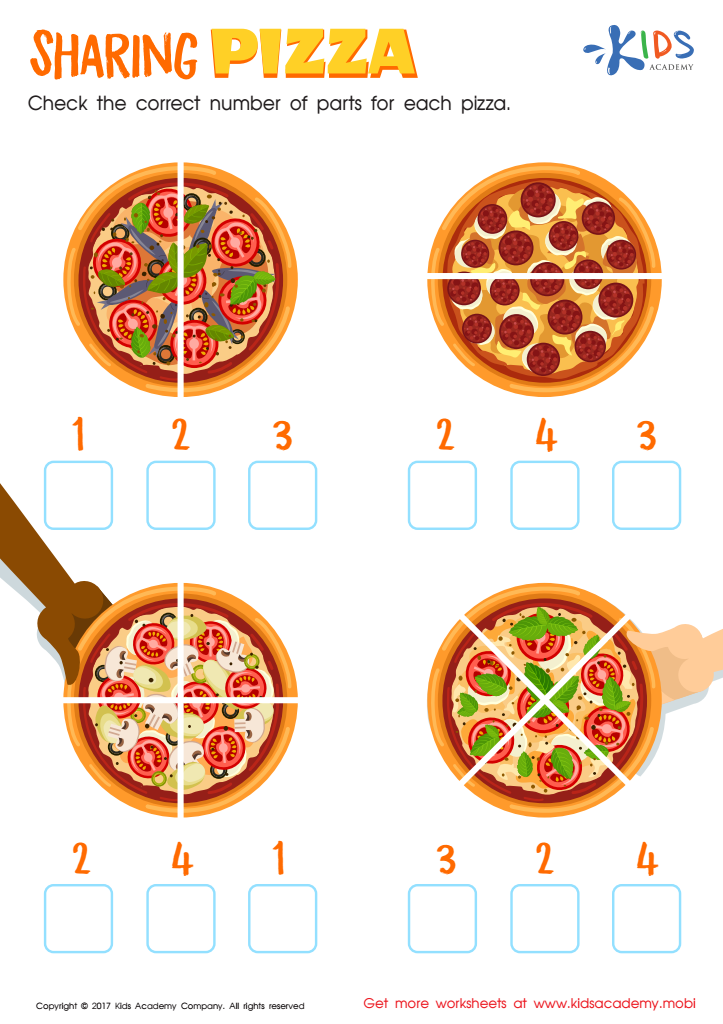

Sharing Pizza Worksheet

Comparing Numerators Part 1 Worksheet
Understanding fractions and comparing numbers is crucial for children aged 5-8 as it lays a strong mathematical foundation. At this developmental stage, children begin to grasp abstract concepts, and mastering these skills fosters critical thinking and problem-solving abilities.
Fractions introduce the idea of part-to-whole relationships, helping children comprehend concepts of division and ratios. Learning to compare numbers enhances their ability to discern greater and lesser values, which is vital for everyday decision-making, such as knowing quantities and prices.
For parents and teachers, reinforcing these concepts can be pivotal in a child’s academic journey. Engaging with fractions and number comparison enhances numeracy skills, ultimately improving performance in more complex mathematics as they grow. It promotes confidence, as children gain proficiency in handling real-world situations involving measurements and sharing.
Moreover, integrating these concepts into fun activities or games keeps learning enjoyable, which is essential for maintaining motivation and a positive attitude toward mathematics. By nurturing these skills early on, educators and caregivers encourage a lifelong appreciation for math, setting children up for success in both academic and real-world contexts. This foundational understanding facilitates seamless transitions into more advanced mathematical concepts in later years.

 Assign to My Students
Assign to My Students